How Does Percent Calculate Your Return?
Percent uses the Internal Rate of Return (IRR) formula to calculate the return displayed on the portfolio page. The purpose of this blog is to provide additional detail on Percent’s IRR calculation and explain the importance of this metric to our investors.
Many investors use a simple metric like return on investment (ROI) to measure their returns. ROI shows the percent difference between the current value of an investment and the original value. However, this formula does not incorporate the timing of returns, making it less suited to accurately measure the performance of Percent investments. Thus, Percent uses a version of IRR to calculate returns.
What is IRR, and why does it matter?
IRR is a measure of the annualized rate of return for a given investment or portfolio. To understand the mathematical concept behind IRR, we must first explain the concept of the time value of money.
The concept of the time value of money is based on the fact that a dollar today is worth more than a dollar in the future, due to the fact that you can earn interest (which compounds) on your invested dollar. In general, you calculate the time value of money by assessing a discount factor of future value to a set of cash flows. The factor is determined by the number of periods the cash flow will be impacted as well as the expected rate of interest for the period.
Present value is the time value of money for a series of future cash flows that calculates the value of those cash flows today. For example, if you want to find the value of $100 to be received one year from now or the value of $1,500 to be received each month for the next two years, you are trying to find the present value.
IRR is the rate of return that equates the present value of an investment’s expected gains with the present value of its costs. It is the discount rate for which the net present value of an investment is zero. In other words, it is the return on your investment, discounted to account for the time value of money. To learn more about the formula used to calculate IRR, see Appendix 1 - IRR formula.
IRR assumes that all cash flows are received on a regular basis - i.e., once per year or once per month. Since the timing of cash flows for various investments on Percent may not be periodic, or on a specific schedule, we use the XIRR calculation.
Why do we use XIRR?
XIRR is a variation of the IRR calculation that assumes non-periodic timing of cash flows. That is, while the IRR calculation shown above assumes that all cash flows are received on a regular, periodic basis, XIRR allows for cash flows with non-periodic and irregular timing. This method of calculation adheres more closely to the timing of payments for multiple concurrent Percent investments. To learn more about the formula used to calculate XIRR, see Appendix 2 - XIRR formula.
What is included in Percent's XIRR calculation?
To calculate returns, we include the cash flows and events related to the deals in which an investor has participated, as well as any interest earned on idle cash.
Realized Transactions
- Initial investment or purchase of position (represented as a negative number in the calculation)
- Payments of interest and principal, net of fees
- Sale of a position
- Interest earned on idle cash balances
Assumed Transactions
- Return of outstanding principal for a given investment assumed to be repaid today. Note that if a deal is charged-off, this amount is reduced by the amount of charged-off principal
The transactions listed above are included for all confirmed investments on Percent, with the exception of deals in the Work-Out state. The reason we exclude Work-Out deals is that we can no longer assume that all principal will be received at maturity, but neither can we assume that all principal will be charged-off as is it a possibility that either all, a portion, or no principal may be repaid. Once an investment moves into either the Repaid or Charged-Off state, it is included in the return calculation once again.
How does the calculation work for all-time returns?
The calculation for all-time returns is straightforward. We include the same realized transactions listed above, with t=0 being your first confirmed investment on Percent. We also include the assumption that all outstanding principal (active and not in Work-Out State) will be repaid as of today while all future interest payments are excluded from the calculation.

This deal paid monthly interest in 2024, and has made its first interest payment of 2025 in the amount of $10. It has not made any principal payments, so the full $1,000.00 of the investor’s principal remains outstanding.
The cash flows to calculate all-time IRR would be:
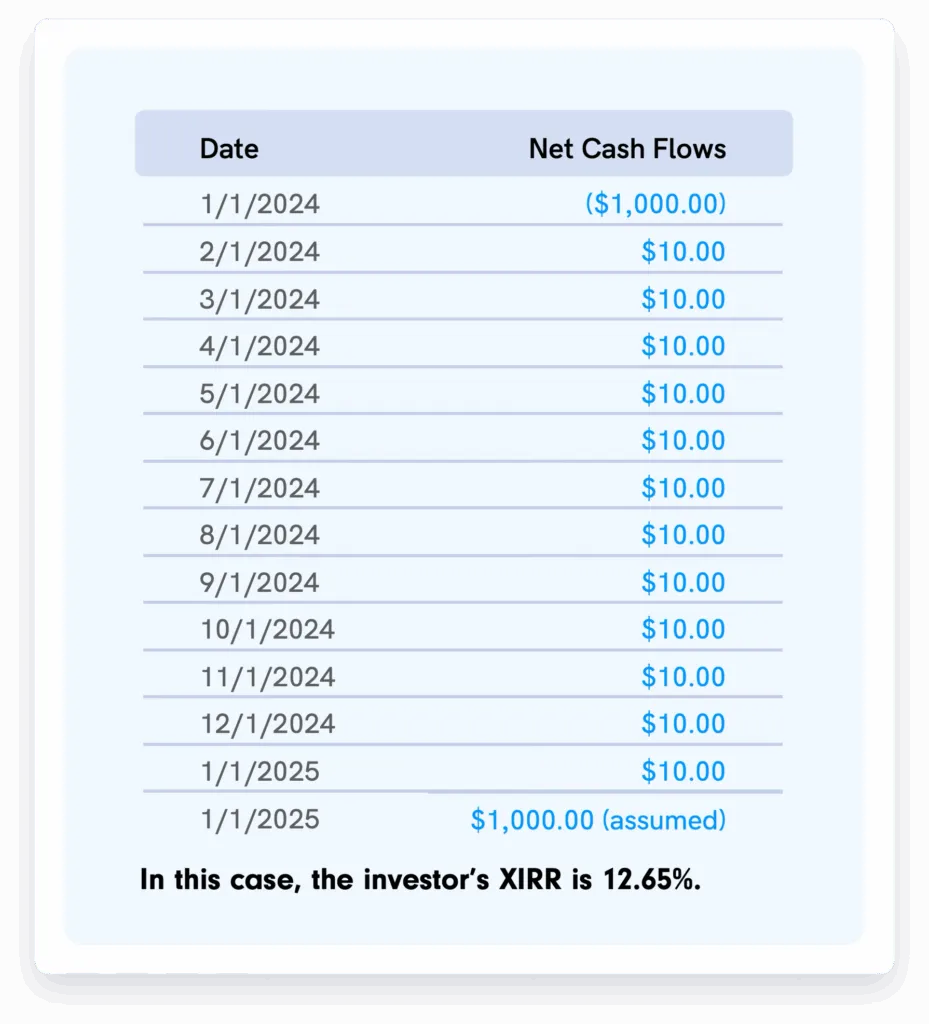
To calculate this yourself, you can enter the dates and cash flows into the XIRR formula in Excel or a financial calculator.
How does the calculation work for Year to Date (YTD)?
YTD is slightly more complex. We include all deals that have either been invested into, received a payment, or received a charge-off in the current calendar year. For those deals, we need a basis upon which to compare the returns, so we also include the initial investment and any return of principal in the calculation, even if that occurred in a prior calendar year. We also assume the return of principal as of today for these deals, consistent with the approach used in our all-time returns calculation.
With that in mind, the earliest transaction included (t=0) in the YTD calculation is the initial investment for the earliest deal that received a payment, charge-off, or investment in the calendar year. To demonstrate, let’s use the same example used above:
- Current Date: 6/30/2025
- Investment Date: 1/1/2024
- Investment Amount: $1,000.00
- Maturity Date: 1/1/2026
This deal paid monthly interest in 2024 and the first half of 2025. It has not made any principal payments, so the full $1,000.00 of the investor’s principal remains outstanding.
Example: The cash flows to calculate YTD 2024 IRR would be:
.webp)
stors. As part of our focus on standardizing private markets, we employ these calculations across our platform so that investors can compare their returns across investments. If you have any questions about the rate of return shown for your investments, we encourage you to contact our Investor Relations experts.
Appendix 1 - IRR Formula
This formula is best solved by using a financial calculator or Excel.
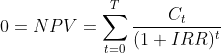
NPV = net present value
T = number of time periods
Ct = total net cash flow during period t
- At t=0, this is your outgoing investment amount (e.g., a negative number)
Appendix 2 - XIRR Formula
This formula is best solved by using a financial calculator or excel.

NPV = net present value
T = number of time periods
Ct = total net cash flow during period t





